傳輸線設(shè)計(jì)是高頻有線網(wǎng)絡(luò)、射頻微波工程、雷射光纖通信等光電工程的基礎(chǔ)，為了能讓能量可以在通信網(wǎng)路中無(wú)損耗地傳輸，良好的傳輸線設(shè)計(jì)是重要關(guān)鍵。 

    無(wú)線通信加上視頻技術(shù)將成為未來(lái)的明星產(chǎn)業(yè)，要達(dá)到這個(gè)目標(biāo)，負(fù)責(zé)傳送射頻微波信號(hào)的介質(zhì)除空氣之外，就是高頻的傳輸線。人類目前無(wú)法控制大氣層，但是可以控制射頻微波傳輸線，只要設(shè)法使通信網(wǎng)路的阻抗能相互匹配，發(fā)射能量就不會(huì)損耗。本文將從阻抗匹配的角度來(lái)解析射頻微波傳輸線的設(shè)計(jì)技術(shù)。
  
    駐波比（SWR）

    兩頻率相同、振幅相近的電磁波能量流（energy flows）面對(duì)面地相撞（impinge）在一起，會(huì)產(chǎn)生駐波（standing wave），這種電磁波的能量粒子在空間中是處于靜止（stand）狀態(tài)（motionless）的，此暫停運(yùn)動(dòng)的時(shí)間長(zhǎng)度比兩電磁波能量流動(dòng)的時(shí)間要長(zhǎng)。因?yàn)轳v波的能量粒子是靜止不動(dòng)的，所以，沒(méi)有能量流進(jìn)駐波或從駐波流出來(lái)。上述敘述較抽象，但是這里舉個(gè)類似的例子，就可說(shuō)明什么是駐波：做個(gè)物理實(shí)驗(yàn)，將兩個(gè)口徑、流速都相同的水管，面對(duì)面相噴，在兩水管之間將會(huì)激起一個(gè)上下飛奔的水柱，這個(gè)水柱就是駐波。如果是在無(wú)地心引力的空間中，這個(gè)水柱將靜止在那里不會(huì)墜地。 

    電磁波在傳輸在線流動(dòng)，入射波和反射波相遇時(shí)就會(huì)產(chǎn)生駐波。駐波比（standing wave rate；SWR）是駐波發(fā)生時(shí)最大電壓和最小電壓的比值（VSWR），或最大電流和最小電流的比值(公式一)：

    SWR = (VO + VR)/ (VO - VR) = (IO + IR)/ (IO - IR) = 1＋｜Γ｜/ 1－｜Γ｜

    WR可以被用來(lái)判定傳輸線阻抗匹配的情況：當(dāng)SWR=1時(shí)，表示沒(méi)有反射波存在，電磁波能量能完全傳遞到負(fù)載上，也就是傳輸線阻抗完全匹配；當(dāng)SWR=∞時(shí)，表示VO = VR或IO = IR，電磁波能量完全無(wú)法傳遞到負(fù)載上，傳輸線阻抗完全不匹配。SWR測(cè)量?jī)x是高頻傳輸線、發(fā)射機(jī)（transmitter）、天線工程師常使用的參數(shù)，與它類似的是應(yīng)用在有線電視纜線（Cable TV cable）的「返回耗損（Return Loss）」或稱作dBRL。兩者的差別有二：(1)dBRL=0表示阻抗完全不匹配，dBRL=∞表示阻抗完全匹配。(2)SWR測(cè)量?jī)x是以發(fā)射機(jī)為信號(hào)來(lái)源，自己并沒(méi)有發(fā)射源，但dBRL測(cè)量?jī)x是用自己的發(fā)射源來(lái)測(cè)量纜線的阻抗匹配情況。

    '史密斯圖（Smith Chart）介紹：

    為了達(dá)到阻抗匹配的目的，必須使用史密斯圖。此圖為P. Smith于1939年在貝爾實(shí)驗(yàn)室發(fā)明的，直到現(xiàn)在，它的圖形仍然被廣泛地應(yīng)用在分析、設(shè)計(jì)和解決傳輸線的所有問(wèn)題上。它能將復(fù)數(shù)的負(fù)載阻抗（complex load impedance）映射（map）到復(fù)數(shù)反射系數(shù)（complex reflection coefficients）的Γ平面上，這種映射過(guò)程稱作「正常化（normalization）」。如(圖一)所示，大小不同的圓弧代表實(shí)數(shù)（rL）與虛數(shù)（xL）的大小，越往右邊阻抗越大，越往左邊阻抗越小。乍看之下，史密斯圖很類似極坐標(biāo)（polar coordinate），不過(guò)，它的X-Y軸坐標(biāo)分別是Γr和Γi，而且Γ= |Γ|ejθr =Γr + jΓi ，r代表實(shí)數(shù)（real number），i代表虛數(shù)（image number）。在圖一中，中心線為電阻值，中心線上方區(qū)域?yàn)楦锌怪担行木€下方區(qū)域?yàn)槿菘怪担睆胶椭行木€重迭的圓代表不同的實(shí)數(shù)（rL），中心線兩旁的圓弧代表不同的虛數(shù)（rL）。正常化負(fù)載阻抗（normalized load impedance）zL = ZL/Z0= 1+Γ/1-Γ，zL= rL+jxL，其實(shí)zL就是史密斯圖上的復(fù)數(shù)，它沒(méi)有計(jì)量單位（dimensionless），是由實(shí)數(shù)rL和虛數(shù)xL構(gòu)成的。負(fù)載阻抗ZL就是由小寫(xiě)的zL映射到復(fù)數(shù)反射系數(shù)Γ平面上的。史密斯圖的圓心代表Γ=0，zL=1，ZL= Z0，負(fù)載阻抗匹配，如(圖三)所示。

    將阻抗轉(zhuǎn)換到Γ平面后，就能得出代表傳輸線匹配或不匹配的反射系數(shù)（公式二）：

    Γ=
    ZL-Z0
    ZL+Z0
　

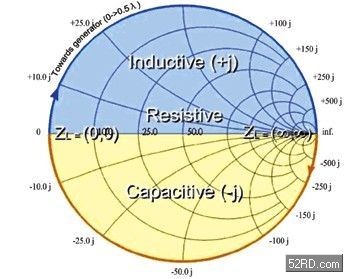
    圖一　史密斯Z坐標(biāo)圖
　

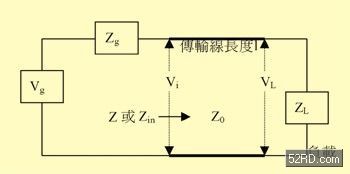
    圖二　無(wú)耗損傳輸線電路
　

    在上式中，Γ就是（電壓）反射系數(shù)，它的定義是：反射波（reflected voltage wave）的電壓振幅與入射波（incident voltage wave）的電壓振幅之比值；ZL是負(fù)載阻抗（load impedance），Z0是特性阻抗（characteristic impedance）。當(dāng)ZL = Z0時(shí)，達(dá)到阻抗匹配，Γ為零。如(圖二)所示，假設(shè)ZL = Z0，電壓源（Vg）產(chǎn)生的功率幾乎可以完全供給負(fù)載使用，而從負(fù)載反射回電壓源的功率非常小。對(duì)負(fù)載應(yīng)用而言，必須設(shè)法求得特性阻抗，并使負(fù)載阻抗等于它。亦即，在圖三中的Γ必須盡量在綠色區(qū)域之中。圖三也稱為珈瑪坐標(biāo)圖（Gamma-centric chart），有別于圖一的Z坐標(biāo)圖（Z- centric chart）。
　

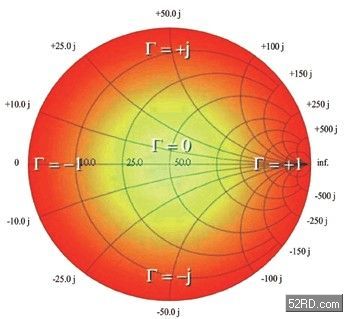
    圖三　史密斯Γ坐標(biāo)圖
　

    理想的無(wú)耗損（lossless）傳輸線是依據(jù)下列公式來(lái)轉(zhuǎn)換負(fù)載阻抗ZL（公式三）：
    Z = Z0
    ZL cos(l 2/) + j Z0 sin(l 2/)
    Z0 cos(l 2/) + j ZL sin(l 2/)

    在上式中，l是無(wú)耗損傳輸線的長(zhǎng)度，l 2/是此傳輸線長(zhǎng)度與波長(zhǎng)相比的角度值（radian）。從上式和圖二中，可以得出下列重要的結(jié)論：

    (1)如果ZL = Z0，則無(wú)論傳輸線的長(zhǎng)度大小為何，輸入端阻抗Z或Zin永遠(yuǎn)等于特性阻抗Z0。

    (2)Z是以/2為單位做周期變化。

    (3)正常化輸入阻抗（normalized input impedance）zin=Zin/Z0= 1+Γl/1-Γl，其中，Γl 的振幅與電壓反射系數(shù)Γ的振幅一樣，但是相角差2βl（β=2π/λ），l是傳輸線長(zhǎng)度。所以，Γl被稱為「相移電壓反射系數(shù)（phase-shifted voltage reflection coefficient）」，而且Γl =Γe-j2βl。因此，如果Γ轉(zhuǎn)換成（transform）Γl，zL就被轉(zhuǎn)換為zin了，在史密斯圖上的反射系數(shù)角位（angle of reflection coefficient in degrees）是以順時(shí)鐘方向，隨傳輸線長(zhǎng)度l由0最大增加到0.5λ，這個(gè)方向上的刻度稱為「波長(zhǎng)朝產(chǎn)生器（wavelengths toward generator；WTG）」方向的刻度，有別于逆時(shí)鐘方向的「波長(zhǎng)朝負(fù)載（wavelengths toward load；WTL）」方向的刻度。

    (4)在史密斯圖的圓心處劃一個(gè)圓，它將和實(shí)數(shù)軸與虛數(shù)軸相交于數(shù)個(gè)點(diǎn)，每個(gè)點(diǎn)與圓心的距離相等，這個(gè)圓稱作「常數(shù)｜Γ｜圓」；也叫作「駐波率（standing-wave ratio；SWR）圓」，這是因?yàn)轳v波率S=1＋｜Γ｜/ 1－｜Γ｜。
如果今天已知傳輸線長(zhǎng)度l和zL，利用史密斯圖，就可以很快地求出zin。

    (5)純電阻窄頻匹配（resistive narrowband match）時(shí)，駐波率剛好等于rL和駐波率圓相交的右邊接點(diǎn)Pmax。雖然rL和駐波率圓相交的接點(diǎn)有兩個(gè)Pmax和Pmin，但是左邊接點(diǎn)Pmin的rL值小于1，而且駐波率必須大于或等于1，所以Pmin不予考慮。藉由史密斯圖和已知的負(fù)載阻抗，就可以很快地求得在傳輸在線最大電壓或最小電流、最小電壓或最大電流的位置。

    上述功能，說(shuō)明了利用史密斯圖就能得到負(fù)載的復(fù)數(shù)阻抗之匹配值。 

    阻抗（impedance）和導(dǎo)納（admittance）的轉(zhuǎn)換

    在解決某些類型的傳輸線問(wèn)題時(shí)，為求方便起見(jiàn)都使用導(dǎo)納來(lái)表示。導(dǎo)納是阻抗的倒數(shù)，其數(shù)學(xué)定義是：Y=1/Z=G+jB，G稱作電導(dǎo)（conductance），B稱作電納。正常化導(dǎo)納y是正常化阻抗z的倒數(shù)，所以y=1-Γ/1+Γ。如果在史密斯圖上順時(shí)鐘移轉(zhuǎn)λ /4（互成反方向），zL將轉(zhuǎn)換成zL。雖然，Y參數(shù)（=[Y][V]）的導(dǎo)納和Z參數(shù)（[V]=[Z]）的阻抗，都只能代表低頻電路的特性，但是與代表高頻電路特性的S參數(shù)（[V-]=[S][V+]）類似的Y參數(shù)是由四種導(dǎo)納變數(shù)構(gòu)成的，藉由Y參數(shù)（一般是從所測(cè)量的S參數(shù)轉(zhuǎn)換而來(lái)）可以得到晶體管閘阻抗之值，這在深次微米設(shè)計(jì)中是非常重要的。S參數(shù)是被用來(lái)表示射頻微波多端口網(wǎng)絡(luò)（multiple network）中多電波的電路特性。 

    ■史密斯圖應(yīng)用范例

    應(yīng)用上述原理和方法，將一般的50-Ω無(wú)耗損傳輸線之一端接有負(fù)載阻抗ZL =（25+j50）Ω，使用史密斯圖可以得到：

    (1)電壓反射系數(shù)：zL= ZL/Z0=（25+j50）/50=0.5+j1，從史密斯圖中可以查出反射系數(shù)的相角為83°，用尺可以量得反射系數(shù)的振幅為0.62；所以，電壓反射系數(shù)Γ= 0.62ej83°。

    (2)電壓駐波比（SWR）：使用圓規(guī)在史密斯圖上，以Γ=0為圓心，劃一個(gè)圓（駐波率圓）通過(guò)0.62ej83°，這個(gè)圓和Γr相交在兩點(diǎn)，其中一點(diǎn)的rL值大于1，為4.26，亦即電壓駐波比S=4.26。

    (3)距負(fù)載最近的最大電壓與最小電壓的位置：最大電壓在駐波率圓和Γr相交的點(diǎn)上，查史密斯圖，此點(diǎn)的位置是0.25λ，負(fù)載的位置是0.135λ，所以它和負(fù)載的距離是lmax=0.25λ-0.135λ=0.115λ；最小電壓和最大電壓的距離差0.25λ，所以它和負(fù)載的距離是lmin=0.115λ+0.25λ=0.365λ。

    (4)若此傳輸線長(zhǎng)度為3.3λ，可求出其輸入阻抗和輸入導(dǎo)納：3.3λ除以0.5λ后剩余0.3λ，從負(fù)載阻抗在史密斯圖上的位置順時(shí)鐘移動(dòng)（WTG）0.3λ，就是輸入阻抗的位置。因此，輸入阻抗的位置是在0.135λ+0.3λ=0.435λ直線上，它與駐波率圓相交于一點(diǎn)，查史密斯圖，此點(diǎn)即是正常化輸入阻抗zin=0.28-j0.4，經(jīng)轉(zhuǎn)換可求得輸入阻抗Z in=zinZ0=(0.28-j0.4)*50=(14-j20)Ω；從zin順時(shí)鐘移動(dòng)0.25λ并與駐波率圓相交于一點(diǎn)，可以得到正常化輸入導(dǎo)納yin=1.15+j1.7，經(jīng)轉(zhuǎn)換可求得輸入導(dǎo)納Yin=yinY0=yin/ Z0=(1.15+j1.7)/50=（0.023+j0.034）S（全名為Siemens，是導(dǎo)納的基本計(jì)量單位）。

    '使用史密斯圖反求負(fù)載阻抗

    假設(shè)：只知道一條50Ω無(wú)耗損傳輸線的駐波比S=3，距負(fù)載最近的最小電壓位置是5cm，其次是20cm，試求負(fù)載阻抗。

    解決方法：因?yàn)樽钚‰妷旱拈g距為λ / 2，所以，λ = 40cm。距負(fù)載最近的最小電壓在史密斯圖上的位置就是5/40=0.125λ。在史密斯圖上劃駐波率圓，半徑為3，此圓與Γr相交于兩點(diǎn)，rL值小于1的點(diǎn)就是距負(fù)載最近的最小電壓，在駐波率圓上，從此點(diǎn)逆時(shí)鐘移動(dòng)0.125λ，可以得到負(fù)載的正常化阻抗zL=0.6 - j0.8。經(jīng)轉(zhuǎn)換后，就可得出負(fù)載阻抗ZL=Z0*zL=(30 - j40)Ω。

    阻抗匹配

    阻抗匹配是電路學(xué)里的重要議題，也是射頻微波電路的重點(diǎn)。一般的傳輸線都是一端接電源，另一端接負(fù)載，此負(fù)載可能是天線或任何具有等效阻抗ZL的電路。傳輸線阻抗和負(fù)載阻抗達(dá)到匹配的定義，簡(jiǎn)單說(shuō)就是：Z0=ZL。在阻抗匹配的環(huán)境中，負(fù)載端是不會(huì)反射電波的，換句話說(shuō)，電磁能量完全被負(fù)載吸收。因?yàn)閭鬏斁€的主要功能就是傳輸能量和傳送電子訊號(hào)或數(shù)字?jǐn)?shù)據(jù)，一個(gè)阻抗匹配的負(fù)載和電路網(wǎng)絡(luò)，將可確保傳輸?shù)阶罱K負(fù)載的電磁能量值能達(dá)到最大量。 

    最簡(jiǎn)單的阻抗匹配方法是設(shè)計(jì)負(fù)載電路使其滿足ZL= Z0的條件。可惜這是理想的情況，在設(shè)計(jì)實(shí)務(wù)上，因?yàn)樨?fù)載電路必須先滿足其它必需的條件，否則負(fù)載電路就無(wú)法提供應(yīng)用所需的性能，這通常都會(huì)影響它和傳輸線的阻抗匹配。解決方案是在傳輸線與最終負(fù)載之間加入阻抗匹配網(wǎng)絡(luò)（impedance-matching network），加入此網(wǎng)絡(luò)的目的就是為了減少傳輸線和此網(wǎng)絡(luò)之間的電波反射作用。如果阻抗匹配網(wǎng)絡(luò)是無(wú)耗損的，而且其輸入阻抗ZL等于傳輸線的特性阻抗Z0，則能量將可以透過(guò)它全部到達(dá)負(fù)載端。

    阻抗匹配網(wǎng)絡(luò)可以由數(shù)個(gè)集成組件（lumped elements）或具有特定長(zhǎng)度和終端方式（短路或開(kāi)路）的數(shù)節(jié)（sections）傳輸線構(gòu)成。若是使用集成組件，通常是選用電容和電感，而不用電阻，這是為了避免奧姆耗損（ohmic losses）。因?yàn)樽杩蛊ヅ渚W(wǎng)絡(luò)必須將負(fù)載阻抗ZL= RL +jXL的RL、XL分別與傳輸線特性阻抗Z0相對(duì)應(yīng)的電阻與電抗值匹配，為了達(dá)到這兩種轉(zhuǎn)換，它至少需要「兩個(gè)調(diào)整參數(shù)」或「兩個(gè)自由度（two degrees of freedom）」。(圖四)是單株短路線（shorted single-stub）阻抗匹配網(wǎng)絡(luò)，其等效電路如(圖五)所示。兩個(gè)自由度是由圖四中，長(zhǎng)度各為d和l的兩節(jié)傳輸線提供的。
　

    圖四　單株短路線阻抗匹配網(wǎng)絡(luò)
　
    因?yàn)榇藛沃曜杩蛊ヅ渚W(wǎng)絡(luò)是以并聯(lián)的方式形成，所以也稱作「分路腳線（shunt stub）」。計(jì)算它時(shí)，使用導(dǎo)納Y會(huì)比使用阻抗Z方便。

    其匹配程序是由兩個(gè)基本步驟構(gòu)成的：(1)選定d的長(zhǎng)度：藉此將負(fù)載導(dǎo)納YL轉(zhuǎn)換成Yd，Yd = Y0 + jB。(2)選定l的長(zhǎng)度：藉此將輸入導(dǎo)納Ys轉(zhuǎn)換等于-jB。

    如圖五所示，因?yàn)閅in= Yd+Ys，所以輸入的等效導(dǎo)納Yin= Y0，這就達(dá)到阻抗匹配的目的了。簡(jiǎn)單地說(shuō)，阻抗匹配網(wǎng)絡(luò)的目的就是要消除輸入阻抗的電抗（reactance）X值。

　



    圖五　單株短路線阻抗匹配網(wǎng)絡(luò)的等效電路
　
    阻抗匹配網(wǎng)絡(luò)設(shè)計(jì)范例

    一條50Ω無(wú)耗損傳輸線一端連接天線，此天線的阻抗是ZL=（25-j50）Ω，試求單株短路腳線的位置和長(zhǎng)度d和l。
解決方法如下：

    (1)求得正常化負(fù)載阻抗zL=ZL/Z0=0.5 - j1，在史密斯圖中可以找到zL的位置。

    (2)以圓規(guī)在史密斯圖上，以zL的振幅為半徑劃駐波率圓。

    (3)在zL相反方向的駐波率圓上，可以找到負(fù)載導(dǎo)納yL=0.4+j0.8，它是位于史密斯圖上順時(shí)鐘0.115λ直線和駐波率圓相交的點(diǎn)上。

    (4)因?yàn)閥in=Yin/Y0，所以yin必須等于1，才能使Yin= Y0，即yin = ys+yd = 1。史密斯圖上的gL=1圓和駐波率圓相交于兩個(gè)點(diǎn)，這兩個(gè)點(diǎn)可以求得兩個(gè)不同的yd，亦即會(huì)有兩組解決方案。查史密斯圖后，可以發(fā)現(xiàn)這兩個(gè)點(diǎn)分別是：1+j1.58、1 - j1.58。

    (5)當(dāng)yin = 1+j1.58時(shí)，它是在史密斯圖順時(shí)鐘0.178λ的位置。d=(0.178-0.115) λ=0.063λ，這就是短路腳線和負(fù)載之間的距離。因?yàn)閥in = ys+yd，所以可以求得ys= -j1.58，位于史密斯圖順時(shí)鐘0.34λ的位置上。因?yàn)槎搪返恼；妼?dǎo)是∞，所以，短路腳在線的正常化負(fù)載電導(dǎo)是位于史密斯圖順時(shí)鐘0.25λ的位置上，短路腳線到分路點(diǎn)的距離l就等于(0.34-0.25) λ=0.09λ。

    (6)同理，當(dāng)yin = 1- j1.58時(shí)，可以求得d=0.207λ、ys= j1.58、l=0.41λ。
雖然，使用離散（discrete）組件也可以達(dá)到阻抗匹配的目的，但是當(dāng)頻率不斷增加或成幾何級(jí)數(shù)衰減時(shí)，傳輸線和腳線（stub）的成本效益比最高。腳線是傳輸線的一小部份，它只是單純地被用來(lái)消除輸入電抗，對(duì)其它電路組件是無(wú)害的。它以兩種身份加入：一是開(kāi)路ZL=∞、一是短路ZL=0。從前面的Z方程式中可以發(fā)現(xiàn)，當(dāng)使用開(kāi)路腳線時(shí)，輸入阻抗等于-Z0cot(l*2/)j，這是一個(gè)電容；當(dāng)使用短路腳線時(shí)，輸入阻抗等于Z0 tan(l*2/)j，這是一個(gè)電感。添加腳線之后，自然就具備了與離散電抗組件（電感和電容）相同的性能，而且效果更好、成本更省。在許多射頻調(diào)諧器（RF tuner）、消除電磁干擾（EMI）、天線的電路中，除了常見(jiàn)到離散電抗組件以外，常常還可以看到一些短短一截的腳線，其目的就是要消除輸入電抗，使輸入阻抗和傳輸線的特性阻抗能夠完全匹配。

    結(jié)語(yǔ)

    上面的計(jì)算，如今大多數(shù)都是使用儀器自動(dòng)測(cè)量，例如：網(wǎng)絡(luò)分析儀（network analyzer）、時(shí)域反射測(cè)量?jī)x（TDR；Time Domain Reflectometry），再經(jīng)軟件運(yùn)算求出。雖然如此，身為射頻微波電路設(shè)計(jì)者必須清楚了解其背后的原理和方法，才能克服隨時(shí)可能發(fā)生的特殊傳輸線問(wèn)題。 

    傳輸線設(shè)計(jì)是高頻有線網(wǎng)絡(luò)、射頻微波工程、雷射光纖通訊等光電工程的基礎(chǔ)，為了能讓能量可以在通訊網(wǎng)路中無(wú)損耗地傳輸，良好的傳輸線設(shè)計(jì)是重要關(guān)鍵。

    國(guó)內(nèi)目前有許多原是模擬產(chǎn)品設(shè)計(jì)制造的業(yè)者，正試圖轉(zhuǎn)型跨入射頻微波電路的領(lǐng)域，例如：電源供應(yīng)器、計(jì)算機(jī)監(jiān)視器、家電、網(wǎng)絡(luò)通訊芯片設(shè)計(jì)等業(yè)者，但是，大都仍然停留在過(guò)去必須向國(guó)外原廠要參考電路圖的習(xí)慣，缺乏如傳輸線設(shè)計(jì)等基礎(chǔ)技能和獨(dú)自開(kāi)發(fā)設(shè)計(jì)的經(jīng)驗(yàn)，這是業(yè)者必須努力自我提升的地方。