我們利用圖9中所示的例子討論在較大級聯分析中如何應用有效噪聲系數。為了計算整個信號鏈的級聯噪聲系數,我們需要將混頻器及其相關的LO和鏡像抑制濾波封裝成一個等效的兩端口網絡,該網絡具有特定的增益和噪聲系數。由于前置濾波器很好地抑制了鏡像頻率下的端點噪聲,所以該兩端口網絡的有效噪聲系數為FSSBe=2(FDSB-1)+1,。
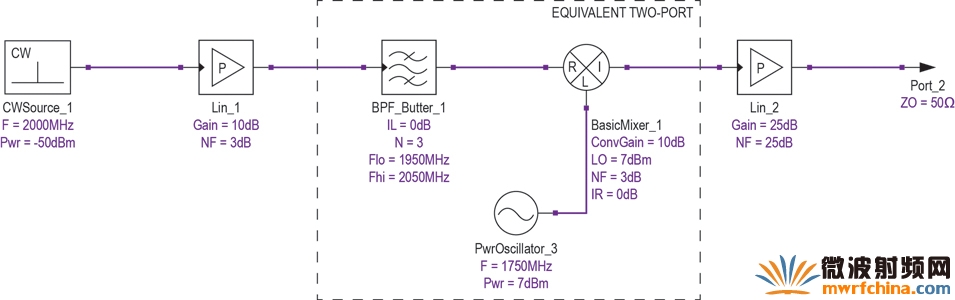
圖9. 外差式混頻器及其相鄰的系統模塊。
注意,適用的噪聲系數既不是混頻器的DSB噪聲系數也不是SSB噪聲系數,而是介于兩者之間的一個有效噪聲系數。這種情況下,DSB噪聲系數為3dB,如上所述,兩端口網絡的等效噪聲系數可計算為4.757dB。將該值帶入總體級聯公式計算,得到系統噪聲系數為7.281dB,如表3所示。手動計算表明,該結果與采用4.757dB計算混頻器噪聲系數的標準弗林斯公式相一致。
表3. 系統中外差式混頻器的仿真級聯性能
| 器件 | CF (MHz) | CNP (dBm) | GAIN (dB) | SNF (dB) | CGAIN (dB) | CNF (dB) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 | 0 |
| Lin_1 | 2000 | -100.975 | 10 | 3 | 10 | 3 |
| BPF_Butter_1 | 2000 | -100.976 | -7.12E-04 | 7.12E-04 | 9.999 | 3 |
| BasicMixer_1 | 250 | -90.563 | 10 | 3 | 19.999 | 3.413 |
| Lin_2 | 250 | -61.695 | 25 | 25 | 44.999 | 7.281 |
一般而言,當用等效兩端口網絡代替混頻器及其相鄰元件時,輸入端口應為被抑制鏡像響應的信號流中的最后節點,輸出端口應為鏡像響應和預期響應組合在一起的最前節點(通常為混頻器的輸出端口)。如果電路結構不能有效抑制混頻器的鏡像響應,則必須修改弗林斯公式才能應用。
零中頻接收機
現在,考慮零中頻或直接轉換接收機(圖10)。
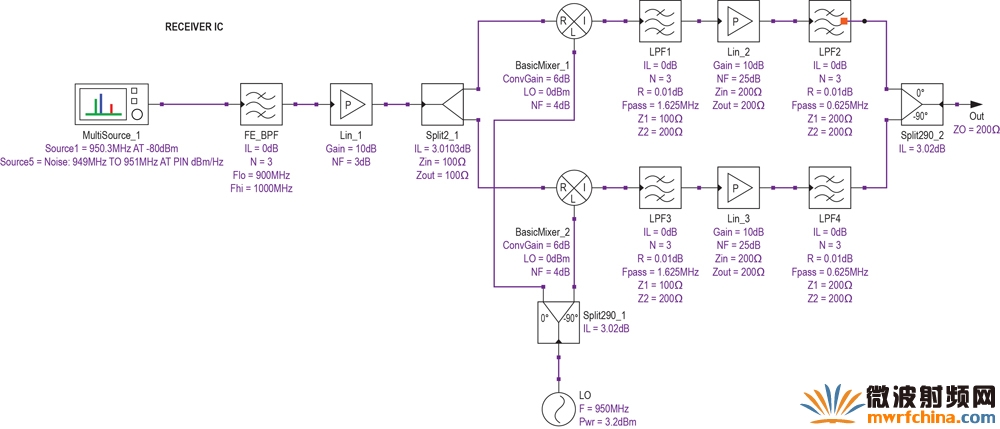
圖10. 帶有LNA、混頻器、濾波器和VGA的ZIF接收機。
配置包括LNA(增益為10dB、噪聲系數為3dB)、帶通濾波器(中心頻率為950MHz)、信號分配器(將信號送至一對混頻器)、一對混頻器(轉換增益均為6dB,DSB噪聲系數為4dB)。VGA設置為10dB增益、25dB噪聲系數。該組合的仿真結果如表4所示。
表4. ZIF接收機配置*
| 器件 | CF (MHz) | CP (dBm) | CNP (dBm) | GAIN (dB) | SNF (dB) | CGAIN (dB) | CNF (dB) |
| MultiSource_1 | 950 | -79.999 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950 | -80.009 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950 | -70.008 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950 | -73.018 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
| BasicMixer_1 | 0 | -67.039 | -99.425 | 5.979 | 4 | 12.959 | 3.81 |
| LPF1 | 0 | -67.04 | -99.425 | -8.23E-04 | 1.00E-02 | 12.958 | 3.81 |
| Lin_2 | 0 | -57.036 | -83.078 | 9.995 | 25 | 22.953 | 10.163 |
| LPF2 | 0 | -57.038 | -83.08 | -1.90E-03 | 1.00E-02 | 22.951 | 10.163 |
*表格中列出的項目有通道頻率(CF)、通道功率(CP)、級增益(GAIN)、級噪聲系數(SNF)、級聯增益(CGAIN)和級聯噪聲系數(CNF)。
注意,在表5中,我們將這一結果與Excel®電子表格利用弗林斯公式計算的級聯噪聲系數進行比較。
表5. 弗林斯級聯公式計算結果
| 器件 | F (dB) | Gain (dB) | CGAIN (dB) | CNF (dB) |
| BPF濾波器 | 0.01 | -0.01 | -0.01 | 0.01 |
| LNA | 3 | 10 | 9.99 | 3.01 |
| 分配器 | 3.01 | -3.01 | 6.98 | 3.22 |
| 混頻器 | 4 | 5.979 | 12.96 | 3.81 |
| LPF1 | 0.01 | -0.01 | 12.95 | 3.81 |
| VGA | 25 | 9.995 | 22.94 | 12.65 |
| LPF2 | 0.01 | -0.01 | 22.93 | 12.65 |
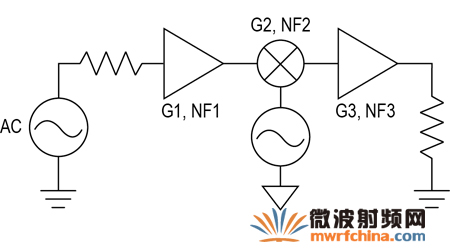
圖11. 包括混頻器的級聯。
輸出的總噪聲密度可計算如下:
NOUT=2kT0G1G2G3+2NA1G2G3+NA2G3+NA3
由于級聯輸入處的熱噪聲引起的輸出噪聲為:
NOT=2kT0G1G2G3.
這意味著總噪聲因子為:
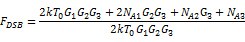
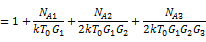
設:
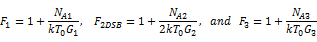
得到:
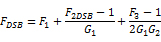
以上推導表明,級聯公式中有必要使用混頻器的DSB噪聲系數;代入計算級聯噪聲系數的一般形式弗林斯公式,隨后所有級的噪聲分布必須除以2。如果后者不除以2,表5中所示的電子表格分析結果是錯誤的。在電子表格中修改公式,將混頻器之后的單元除以2,得到的結果如表6所示。
表6. DSB級聯公式的結果
| 器件 | F (dB) | Gain (dB) | CGAIN (dB) | CNF (dB) |
| BPF濾波器 | 0.01 | -0.01 | -0.01 | 0.01 |
| LNA | 3 | 10 | 9.99 | 3.01 |
| 分配器 | 3.01 | -3.01 | 6.98 | 3.22 |
| 混頻器 | 4 | 5.979 | 12.96 | 3.81 |
| LPF1 | 0.01 | -0.01 | 12.95 | 3.81 |
| VGA | 25 | 9.995 | 22.94 | 10.17 |
| LPF2 | 0.01 | -0.01 | 22.93 | 10.17 |
現在,表6和表4非常一致。然而,這也說明了在涉及到混頻器時直接帶入弗林斯級聯公式計算是不合理的。
現在,我們考慮相同的情況,但預期信號比LO高300kHz。方框圖仍然同圖10所示,但全部信號位于LO的高邊,這就使其成為相同接收機架構的低中頻(LIF)應用。與之前一樣,采用相同的Genesys仿真配置,結果如表7所示。
表7. LIF接收機仿真結果
| 器件 | CF (MHz) |
CP (dBm) |
CNP (dBm) |
GAIN (dB) |
SNF (dB) |
CGAIN (dB) |
CNF (dB) |
| MultiSource_1 | 950.3 | -79.999 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950.3 | -80.009 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950.3 | -70.008 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950.3 | -73.018 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
| BasicMixer_1 | 0.3 | -67.067 | -96.335 | 5.938 | 4 | 12.918 | 6.94 |
| LPF1 | 0.3 | -68.467 | -96.458 | -1.64E-03 | 1.00E-02 | 12.916 | 6.819 |
| Lin_2 | 0.3 | -58.832 | -80.068 | 9.969 | 25 | 22.885 | 13.241 |
| LPF2 | 0.3 | -58.483 | -80.072 | -4.68E-03 | 1.00E-02 | 22.88 | 13.241 |
除噪聲系數增加了3dB之外,結果與之前相同架構的仿真結果相似。實際上,即使該系統中除源電阻之外的全部器件均無噪聲,噪聲系數也將為3dB。從本質上講,這是復合接收機架構的一種SSB應用,無法抑制非預期單邊帶。級聯噪聲系數的推導與以上所述完全相同,但級聯輸入處的熱噪聲引起的輸出噪聲為:
Not=kT0G1G2G3.
所以現在變為:

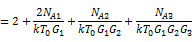
設:
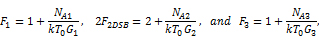
得到:
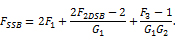
與預期一樣,對于這種結構的DSB應用,噪聲級聯公式中的每一項乘以2。然而,這種情況有時候是不正確的。現在,我們以一臺接收機為例,就噪聲和干擾而言,受兩個邊帶的影響,但僅使用其中一個邊帶的信號。由于下邊帶僅影響易受干擾的接收機,通常采用正交通道來抑制不希望的邊帶信號。一種方法是在接收機的輸出利用90度合成器組合I和Q信號,從而抵消不希望邊帶中的信號,并將其有效增加至預期邊帶。實際上,這將把整個接收機變成一臺鏡像抑制下變頻器。如果能夠在合成點有效地控制被合成信號的相位,最后的和成級將恢復之前失去的3dB系統噪聲系數。圖12中所示為這種方法的一個仿真原理圖,對應結果如表8所示。
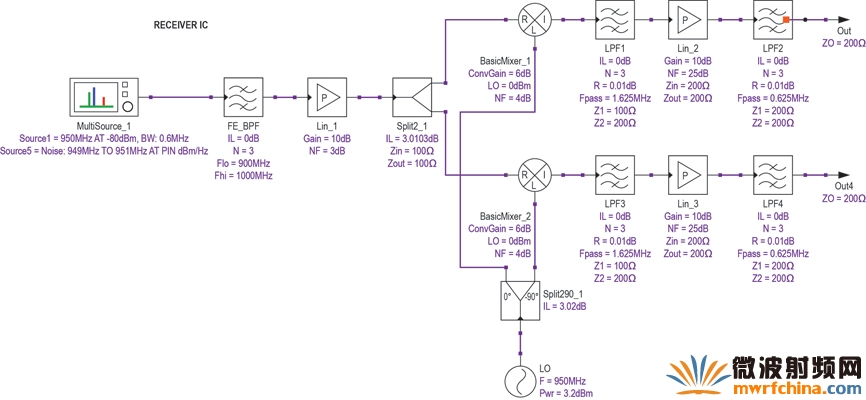
圖12. 帶鏡像抑制的NZIF接收機。
表8. LIF接收機鏡像抑制仿真結果
| 器件 | CF (MHz) |
CP (dBm) |
CNP (dBm) |
GAIN (dB) |
SNF (dB) |
CGAIN (dB) |
CNF (dB) |
| MultiSource_1 | 950.3 | -79.995 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950.3 | -80.005 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950.3 | -70.004 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950.3 | -73.014 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
| BasicMixer_1 | 0.3 | -67.053 | -96.441 | 5.958 | 4 | 12.938 | 6.815 |
| LPF1 | 0.3 | -67.055 | -96.443 | -1.64E-03 | 1.00E-02 | 12.936 | 6.815 |
| Lin_2 | 0.3 | -57.047 | -80.09 | 9.991 | 25 | 22.927 | 13.177 |
| LPF2 | 0.3 | -57.051 | -80.094 | -3.82E-03 | 1.00E-02 | 22.923 | 13.177 |
| Split290_2 | 0.3 | -54.062 | -80.145 | 3.001 | 3.02 | 25.923 | 10.125 |
最后(合成)級的級聯噪聲系數(CNF)改善了3dB,說明噪聲系數恢復,正如預期那樣。
級聯接收機的噪聲系數計算總結
我們已經看到,當接收機級聯中存在混頻器時,計算級聯噪聲因子的弗林斯公式并不總是有效的,無論是使用混頻器的DSB噪聲系數還是SSB噪聲系數。當使用濾波器消除接收機的大部分鏡像響應時,可用一個等效兩端口網絡代替混頻器、濾波器和LO子系統。然而,必須利用DSB噪聲系數計算產生的噪聲系數,考慮耦合到混頻器輸入端口的源端點的頻率選擇性。
我們也發現相同的物理結構會具有不同的有效噪聲系數,取決于信號分布在LO兩側還是一側(即應用是DSB還是SSB)。通過正確使用鏡像抑制合成、復合濾波或等效基帶處理,能夠(通常是)恢復由于復合接收器工作在低中頻(LIF)模式而損失的3dB SNR。
利用Agilent® Genesys程序對這些架構和情況的仿真結果與數學推導得出的級聯噪聲系數相一致。
表9中匯總了本部分討論和仿真的每種架構的級聯噪聲因子。
表9. 推導公式匯總
| 結構 | 應用 | 級聯噪聲因子公式 |
| 三個增益模塊 | 任意 | 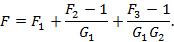 |
| 外差式混頻器 | SSB,理想鏡像濾波器 | 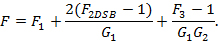 |
| 復合下變頻器 | ZIF | 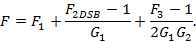 |
| 復合下變頻器 | LIF,無鏡像抑制 | 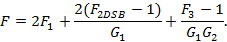 |
| 復合下變頻器 | LIF,鏡像抑制合成 |  |
參考文獻
1 “Mixer Thermal Noise Figure,” Agilent Genesys Documentation,
2 “IRE Standards on Electron Tubes:Definitions of Terms, 1957,” Proceedings of the IRE, vol. 45, pp. 983 –1010, July 1957.tp=&arnumber=4056638&isnumber=4056624
3 Maas, S., Microwave Mixers., Artech House Microwave Library, Artech House, 1993.
4 “Telecommunications:Glossary of Telecommunication Terms,” Federal Standard 1037C,
本文為MWRF.NET獨家專稿,未經允許不得轉載,如需轉載請聯系market#mwrf.net(#換成@)

 粵公網安備 44030902003195號
粵公網安備 44030902003195號