導(dǎo)讀

超材料是通過設(shè)計亞波長結(jié)構(gòu)單元的幾何形狀與排列，實現(xiàn)新奇、特奇性質(zhì)的復(fù)合材料。早在1990年John B. Pendry提出使用亞波長開口諧振環(huán)實現(xiàn)負(fù)磁導(dǎo)率的結(jié)構(gòu)單元時，就提到該結(jié)構(gòu)具有獨特的非線性特征^[1]。此后，關(guān)于超材料的非線性特性的研究在光波段被廣泛研究報道。但是，這些基于金屬單元的超材料通常面臨著高熱損耗以及輻射損耗造成非線性轉(zhuǎn)換效率低的問題。而熱損耗是由金屬的固有性質(zhì)造成的，難以避免，因此減小線性輻射損耗是提高非線性轉(zhuǎn)換效率的重要手段。最近安徽大學(xué)黃志祥教授、愛荷華州立大學(xué)Costas M. Soukoulis教授與浙江大學(xué)沙威研究員課題組提出一種新的物理概念和工程設(shè)計：利用介質(zhì)波導(dǎo)的暗態(tài)模式驅(qū)動磁性超材料開口諧振環(huán)（Split Ring Resonators，SRRs）結(jié)構(gòu)單元，從而實現(xiàn)線性輻射損耗消除，并采用時域有限差分法數(shù)值求解麥克斯韋-流體動力學(xué)多物理場方程^[2,3]，理論上證實了該設(shè)計可顯著提高非線性過程的轉(zhuǎn)換效率。相關(guān)成果以“Nonlinearity in the dark: Broadband terahertz generation with extremely high efficiency”為題發(fā)表在《Physical Review Letters》雜志上(doi:10.1103/PhysRevLett.122.027401)^[4]。論文第一作者為方明博士，申念海研究員、黃志祥教授為論文共同通訊作者。

背景

使用非線性晶體（如GaAs/GaP/GaSe/LiNbO3/ZnTe等）光整流效應(yīng)產(chǎn)生太赫茲信號，是一種產(chǎn)生寬帶太赫茲源的常用手段。兩束頻率不同的光在這些非線性介質(zhì)中傳播時會發(fā)生“混合”，從而產(chǎn)生和頻振蕩與差頻振蕩現(xiàn)象。當(dāng)入射波為脈沖光束時，光束可以分解為一系列單色光疊加；在非線性介質(zhì)中，這些單色分量將會發(fā)生混合。和頻振蕩效應(yīng)產(chǎn)生頻率接近于二次諧波的光波，而差頻振蕩效應(yīng)則產(chǎn)生一個低頻電極化場，這些低頻電極化場可以輻射直到太赫茲的低頻電磁波。通常，這些晶體利用體非線性（Bulk Nonlinearity）效應(yīng)可以通過增長晶體尺度來增加非線性轉(zhuǎn)換效率，但同時需要嚴(yán)格的相位匹配（quasi-phase-matching condition），同時還需要考慮尺度增加帶來的強吸收帶引起的太赫茲頻譜不連續(xù)。為了克服非線性晶體太赫茲源存在的問題，2014年由美國能源局埃姆斯實驗室Costas M Soukoulis教授與Jigang Wang教授課題組提出使用金屬超表面非線性效應(yīng)產(chǎn)生寬帶太赫茲信號^[5]。通過實驗測量與理論分析^[6]，使用金屬超表面產(chǎn)生的太赫茲信號帶寬只受入射激光帶寬影響，頻譜在太赫茲頻段光滑連續(xù)。但是考慮到晶格中心對稱的金屬材料的表面非線性效應(yīng)，且只利用了超表面結(jié)構(gòu)的局域表面等離子體共振模式（Localized Surface Plasmon Resonance，LSPR）增強非線性，其太赫茲轉(zhuǎn)換效率與非線性晶體相比較弱。這是由于超材料本身的熱損耗與輻射損耗較大，因而大大減弱了其局域場大小，造成非線性轉(zhuǎn)換效率低。

創(chuàng)新研究

本研究工作中，研究人員提出了一種提高金屬超表面二階非線性轉(zhuǎn)換效率機制，利用激發(fā)介質(zhì)波導(dǎo)TE2,0暗態(tài)模式（Dark State）驅(qū)動超材料結(jié)構(gòu)單元，可有效的減少設(shè)計超表面的線性輻射，從而大大提升二階非線性轉(zhuǎn)換效率。圖1為非線性超表面設(shè)計原理，利用介質(zhì)波導(dǎo)色散曲線確定暗態(tài)模式所需波導(dǎo)寬度，再利用金屬層量化波導(dǎo)模式控制激發(fā)頻率。由于暗態(tài)模式無法被正入射平面波激勵，這里使用兩個SRR作為交換入射波能量到暗態(tài)模式的天線。由于暗態(tài)模式驅(qū)動，超表面可以看做等效電表面和等效磁表面，通過調(diào)節(jié)兩個SRR的位置，可以調(diào)節(jié)等效電、磁表面的等效電導(dǎo)率與磁導(dǎo)率，如圖2所示。當(dāng)時，整個系統(tǒng)表現(xiàn)為完全吸收體，線性輻射損耗為零。

通過優(yōu)化SRR的位置，如圖3所示，線性輻射損耗接近于零。從傳輸、反射、吸收譜線與結(jié)構(gòu)中的電場分布可以看出：由于暗態(tài)模式的分布，基波能量主要被兩個SRR吸收。對于非線性響應(yīng)，由于SRR結(jié)構(gòu)的幾何對稱破壞將會產(chǎn)生二階非線性效應(yīng)，該二階非線性響應(yīng)與線性電流及極化電荷關(guān)系為jρ(如圖4所示)。因此兩個SRR二階非線性響應(yīng)同步可相干疊加，研究人員所提出的超表面相較于普通SRR超表面二階非線性轉(zhuǎn)換效大于近100倍。

創(chuàng)新點：

(1)本文提出了新的金屬超表面結(jié)構(gòu)，驅(qū)動暗態(tài)模式，消除線性輻射損耗，從而提高了非線性轉(zhuǎn)換效率；
(2)全文的理論分析依賴基于時域有限差分法(Finite-Different Time-Domain, FDTD)的多物理場求解器，為黃志祥教授和沙威研究員課題組合作開發(fā)的自主軟件平臺。該平臺數(shù)值求解麥克斯韋（Maxwell）與流體動力學(xué)（Hydrodynamic）的耦合模型，對金屬非線性電磁效應(yīng)進行全波仿真。

圖文速覽

圖1、暗態(tài)模式超材料示意圖

a、超材料單元及尺寸示意圖，綠色部分為介質(zhì)硅層，其中黑色尖頭表示暗態(tài)模式電場分布；
b、介質(zhì)層TE模式色散關(guān)系曲線，紅圈表示在1550 nm取TE_2,0模式對于介質(zhì)板長度。

圖2、線性輻射損耗減少原理

a、受暗態(tài)模式驅(qū)動，兩個SRR分布在TE_2,0模式兩側(cè)，線性響應(yīng)相反導(dǎo)致具有相反的磁偶級子模式，線性輻射相互抵消。同時可以將超材料分解為等效電流、磁流表面，通過調(diào)節(jié)SRR位置可以控制等效面的電導(dǎo)率與磁導(dǎo)率。
b,c、等效電導(dǎo)率，等效磁導(dǎo)率隨兩個SRR位置變化掃描圖。

圖3、線性響應(yīng)優(yōu)化設(shè)計結(jié)果

a、線性輻射損耗隨著兩個SRR位置變化掃描圖，黑色點為線性損耗最低點；
b、最優(yōu)配置下，超表面?zhèn)鬏敗⒎瓷渑c吸收曲線，灰色陰影為兩個SRR熱損耗值；
c、最優(yōu)配置下，xoz剖面電場分布，可以清晰看到TE_2,0暗態(tài)模式分布。

圖4、應(yīng)用示意圖

a、由于差頻效應(yīng)超材料產(chǎn)生太赫茲信號與傳統(tǒng)SRR超表面對比太赫茲信號增強倍數(shù)；
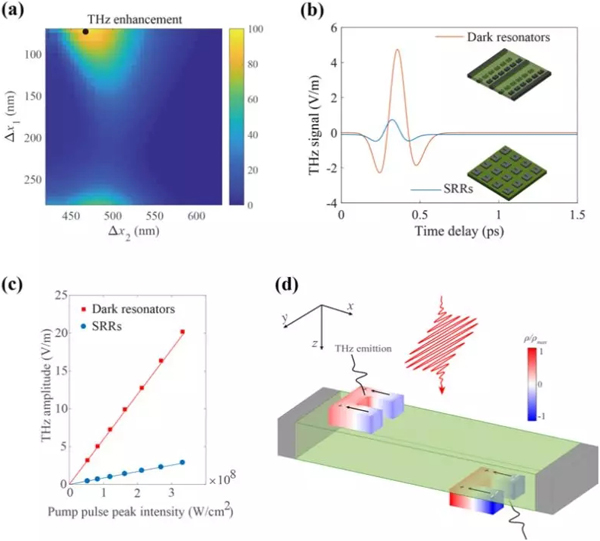
b、暗態(tài)模式超材料與SRR超材料產(chǎn)生太赫茲信號時域圖對比；
c、隨著入射泵浦激光場變化暗態(tài)模式超材料與SRR產(chǎn)生太赫茲信號變化趨勢；
d、太赫茲頻段(4 THz)兩個SRR上非線性響應(yīng)示意圖，可以看出由于為二階非線性兩個SRR響應(yīng)可相干疊加。

參考文獻

[1] Pendry J B, Holden A J, Robbins D J, and Stewart W J. Magnetism from conductors and enhanced nonlinear phenomena[J]. IEEE Transactions on Microwave Theory and Techniques, 1999, 47(11): 2075-2084.
[2] Fang M, Huang Z, Sha W E I, Xiong X Y Z, and Wu X. Full hydrodynamic model of nonlinear electromagnetic response in metallic metamaterials (Invited Paper)[J], Progress In Electromagnetics Research, 2016, 157: 63-78.
[3] Fang M, Huang Z, Sha W E I, and Wu X. Maxwell-Hydrodynamic Model for Simulating Nonlinear Terahertz Generation from Plasmonic Metasurfaces[J], IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2017, 2: 194-201.
[4] Fang M, Shen N-H, Sha W E I, Huang Z, Koschny T, and Soukoulis C M. Nonlinearity in the dark: Broadband terahertz generation with extremely high efficiency[J], Physical Review Letters, 2019, 122: 027401.
[5] Luo L, Chatzakis I, Wang J, Niesler F B P, Wegener M, Koschny T, and Soukoulis C M. Broadband terahertz generation from metamaterials[J]. Nature Communications, 2014, 5(1): 3055.
[6] Fang M, Niu K, Huang Z, Sha W E I, Wu X, Koschny T, and Soukoulis C M. Investigation of broadband terahertz generation from metasurface[J]. Optics Express, 2018, 26(11): 14241-14250.